There are many factors that influence how easily data subjects can be identified in a given data set. For example, whether potentially motivated actors have access to a data set or whether it is protected by confidentiality strongly influences the potential of identification. In the context of pseudonymization and anonymization, another factor is highly prominent, namely the identification potential of the data themselves.
While it is difficult to quantify the identification potential of data, the present section gives an overview of transformations that yield a new data set with reduced identification potential. The more detailed version of this analysis[1] provides further detail. Alternative surveys of methods are for example provided by S. Garfinkel (published by NIST)[2] and Fung et al.[3].
The aspect of identification that is relevant here is that of linking of two (information or) data sets. Different kinds of information elements in the data sets permit different kinds of linking. This is why the following discussion is structured according to kinds of information elements.
In all the described scenarios, the linking takes place between two sets of data (or information). One of these is an asset directly available to the actor who identifies; the other constitutes the personal data (or information) for which identification shall be impeded or ideally prevented. The presented measures modify this latter data set in ways that reduce its potential of identification. The latter data set, in its state before such modification, will be called original data set in the following discussion.
Prevention of deterministic linking of unique handles
The most straightforward manner of linking records of two independent data sets is deterministic linking based on the comparison of unique handles. For this to work, both data sets obviously need to contain handles belonging to the same identity domain. The objective of preventing such linking is therefore to avoid that the data set contains any handles from identity domains used elsewhere.
Starting from an original data set that may contain unique handles from other identity domains, there are two ways of eliminating this:
- Deletion of all unique handles from the data set;
- Replacement of unique handles with unique handles (aka pseudonyms) from a newly created identity domain.
Deletion evidently prohibits linking. Also the replacement of unique handles with ones that are newly created within a new identity domain prevents any linking on equality to other data sets.
The replacement of unique handles can take two strategies. Namely, the newly created unique handle can be:
- independent of original unique handles;
- For example, random numbers.
- derived from the original unique handles.
- In a manner that allows inversion.
- For example, through encryption of a unique handle where the inversion is the decryption of the new handle.
- In a manner that does not allow inversion.
- For example when using a one-way function with a secret key, such as an HMAC.
- In a manner that allows inversion.
A more detailed discussion of options can be found in the ENISA report on pseudonymization[4].
Prevention of linking of quasi-identifiers
Another very common way of linking two data sets is by performing deterministic or probabilistic linking based on quasi-identifiers. Such linking is not guaranteed to be unique for all data records and probabilistic linking usually leaves a certain uncertainty, but typically, such linking can be used to link and thus identify a significant subset of data subjects.
To impede or prevent such identification, the uniqueness of the quasi-identifiers must be reduced. The most common measures used to achieve this are the following:
- Deletion of parts or the whole of a quasi-identifier such that the remainder of the quasi-identifier becomes less unique;
- Generalization of the values that the quasi-identifier is composed of.
The latter measure of generalization is based on the idea of reducing detail in the data and result in a “coarser” data set such that distinctions of data subjects based on details are no longer possible. More precisely, generalization maps multiple possible original values to a single “coarser” value. The objective is that multiple modified quasi-identifiers map to a single, coarser, value and thus make data subjects indistinguishable from one another. This is illustrated by the following examples:
- To generalize a ratio-scale[5] value, an interval of original values is mapped to a single output value. For example, sets of 356 possible dates of birth are mapped to a single year of birth. Similarly, it is possible to map the age of a person to a “generation” such as baby boomers, generation X, and millennials[6]. The latter illustrates that the intervals do not need to be regular.
- Ordinal-scale[7] values can be generalized by grouping adjacent values. A common example for this are 5-digit ZIP codes that are grouped depending on their first two digits. For example, the ZIP code 04609 of Bar Harbor, Maine, could be mapped to 04***.
- Nominal-scale[8] values can be generalized by forming categories. For example, a person’s nationality such as Italian, Spanish, German, etc. could be assigned to the category European.
- It is also possible to generalize multiple attributes together. For example, two attributes create a two dimensional space of possible values. To generalize the two-dimensional values, this space can then be partitioned into areas. This is equivalent to defining intervals in a single dimension. It is illustrated in the following Figure 4 that was taken from Kristen LeFevre et al.[9].
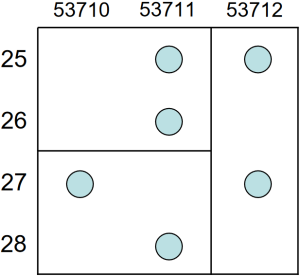
Figure 4: Example of a two-dimensional generalization with ZIP code and age by LeFevre et at.
The most common method to assess whether deletion and generalization in quasi-identifiers sufficiently impedes linkability is k-anonymity[10] by Samarati and Sweeney. In particular, the method consists of verifying that every generalized quasi-identifier occurs at least k times in the data set. This evidently introduces ambiguity into the possible linking. Any link attempt yields at best a set of k undistinguishable candidates for the matching data subject.
When for a chosen k, k-anonymity has not been reached, there are two options for how to proceed:
- Modify the generalization in a way that k-anonymity can be reached. This can for example be done by changing interval boundaries or categorizations.
- Delete the data records whose generalized quasi-identifiers fail to reach the k-threshold. This is sometimes called record suppression[11].
Prevention of linking of identity-relevant properties
In addition to linking based on unique handles and quasi-identifiers, linking is also possible based on unique combinations of values of identity-relevant properties. More precisely, the following section considers both, identity-relevant properties together with (the possibly already generalized) quasi-identifiers.
Also here, the idea behind impeding or preventing linking is based in reducing the uniqueness of data records.
The following discussion is based on a literature review of technical methods to achieve this. Keywords for this literature include among others anonymization, de-identification (and re-identification), disclosure control, and privacy preserving publishing. It is impossible here to provide a comprehensive overview of the wealth of technical methods found in the literature; there are too many methods and many of them come in different variations and combinations. For this reason, the following attempts to provide a categorization of the abstract concepts of transformation that underlie these technical methods.
When looking at data as a model of the world, these concepts of transformation have a certain effect on these models. At the highest level of the categorization, this view permits to distinguish two kinds of concepts:
- Concepts that result in “truthful”, yet less detailed, models of the world, and
- concepts that result in models of the world that deviate from the truth but are close to the truth and possibly even share certain properties with the truth.
This distinction is used to structure the discussion of concepts of transformation.
Truthful concepts of transformation
The following describes truthful concepts of transformation.
Deletion
This concept of transformation is also called suppression and non-disclosure. It reduces detail in the original model by leaving out certain information; the remaining data constitute a truthful model.
Deletion can affect different data elements:
- A single attribute belonging to a single data subject when a value of an attribute becomes too rare (e.g., a very high age).
- A single attribute across all data subjects, i.e. in tabular data, this would delete a whole column.
- All attributes belonging to a single data subject, for example when certain data subjects are easily recognized due to a very rare and identifying combination of values.
- All attributes belonging to a group of data subjects (aka cell suppression), for example when for a given cell k (of k-anonymity) cannot be reached.
- Resampling of time series.
Generalization
Generalization was already discussed above for quasi-identifiers. The same transformation concept can be applied also to identity-relevant properties.
The following distinguishes different kinds of generalization:
- Generalization that apply coarser scales of measurement to one or several attributes in individual-level data, for example:
- Rounding a precise continuous value to a lower precision.
- Aggregating sets of nominal-scaled values into categories.
- Grouping point locations (e.g., latitude and longitude) into areas (such as ZIP code areas, census districts, provinces, or countries).
- Generalization that maps multiple attributes of a single data subject to coarser statistical attributes, for example:
- A time series of a patient’s body temperature mapped to the average, minimum, and maximum temperature.
- Generalization that maps attributes of multiple data subject to a single attribute describing groups of data subjects:
- Statistics.
Note that it may be common to think that it was impossible to link statistical data to individual-level data sets; in other words, that statistical data were free of risk of identification. As is described well by Garfinkel et al.[12], this is not always the case. In particular, if a multitude of statistics is available, a so called reconstruction attack may be possible. In their paper, Garfinkel et al. provide a practical example for this. They show how in certain cases, it is possible to reconstruct original value of some or even all data subjects.
Slicing
It has been argued above that multi-dimensional data has a higher risk of containing unique combinations of attributes for data subjects. Multi-dimensional data sets therefore have a high potential for linking. Slicing addresses the risk inherent in multi-dimensionality.
The concept of slicing takes a multi-dimensional original data set and splits it into multiple pieces, each of which being only of a small dimension. These pieces still contain individual-level data.
The linkability of records across pieces is then controlled carefully. This is typically done by forming groups of data subjects (typically based on generalization of quasi-identifiers) and adding a group number as additional attribute in every piece. Typically, that results in pieces where every group contains at least a certain number (k) of data subjects, very similar to k-anonymity.
Examples of slicing include the following:
- Anatomization proposed by Xiao and Tao[13].
- KC-slice method by Onashoga et al.[14] that was further refined by Raju et al.[15].
Note that slicing does not by itself guarantee to prevent linking of data sets. But by breaking up high-dimensional data sets into multiple smaller-dimensional ones, it reduces the risk of highly identifying unique combinations.
Concepts of transformation that introduce deviations from the truth
This section provides an overview of transformations that introduce deviations from the truth.
Top- and bottom-coding
Top- and bottom-coding avoids identification based on rare very high or very low ratio values, respectively. For this purpose, a threshold is chosen and every value higher or lower than the threshold, respectively, is replaced by the threshold value. For example, 90 may be chosen as a threshold age and all age values greater than 90 in the data set are replaced by 90. Top- and bottom-coding are routinely used in statistical publications such as census data[16].
Data swapping
The basic concept of data swapping is that data values are randomly swapped between individuals contained in a data set. Typically, such swapping is restricted to individuals belonging to the same “group” or “cell”. For a more detailed discussion of data swapping, see for example Fienberg and McIntyre[17]. A description how data swapping was used in the U.S. 1990 census is provided by McKenna[18].
Random noise injection
In noise injection (aka noise addition), a random error is added to truthful data. The more error is added, the less likely that identification is still possible
The key question with noise injection is how much noise needs to be added to prevent identification. The probably best-known approach to answering this question is differential privacy that was first proposed by Dwork et al.[19]. According to Sartor[20], “[m]any privacy researchers regard [differential privacy] as the ‘gold standard’ of anonymization”. This may largely be since “it offers a guaranteed bound on loss of privacy due to release of query results, even under worst-case assumptions”[21]. Referencing Dwork et. al[22], Wikipedia states: “Although it does not directly refer to identification and reidentification attacks, differentially private algorithms probably resist such attacks.”[23] This statement seems to be further supported by McClure and Reiter[24].
Sartor provides a good introduction to the topic and lists further introductory resources; a more detailed introduction was provided by Wood et al[25].
Differential privacy is not a single transformation to reduce the identification potential of a data set. In fact, differential privacy is a mathematical framework that is based on a mathematical definition of what privacy actually is. There are hundreds of published differentially private mechanisms for which there are mathematical proofs that comply with the mathematical framework. Examples include building a histogram[26], taking an average[27], releasing micro-data[28] (i.e., individual-level data), and generating a machine learning model[29].
Differential privacy is a complex topic and requires a high level of mathematical skill to be understood and thus used. The Linknovate Team has conducted a survey in 2018 and found that only very large players are typically engaged in differential privacy activities[30]. Among the most prominent practical applications of differential privacy is the Census 2020[31] by the U.S. Bureau of the Census and the mining of user data by Apple[32] [33]. But neither of these have yet proven to be success stories.
Sartor concludes his experience by saying that differential privacy was “beautiful in theory” but a “fallacy in practice[34]. In more detail, he writes:
“Differential privacy is a beautiful theory. If it could be made to provide adequate utility while maintaining small epsilon, corresponding complete proofs, and reasonable assumptions, it would certainly be a privacy breakthrough. So far, however, this has rarely, and arguably never happened.”
Key aspects of transformations that reduce the identification potential of data
This section provides a summary of the above presented transformation concepts to reduce the identification potential of data sets. It points out some important characteristics that help understand how to apply the transformations and what guarantees they can provide that identification is no longer possible.
- Most of the above described concepts of transformation fail to consider the data set as a whole but rather have a limited scope. For example, top-coding considers only a single attribute value of a single individual, and generalization in the context of k-anonymity focuses exclusively on the linking of the data elements that compose a quasi-identifier (while leaving all the other data elements unaffected).
- Transformations of data sets lead to a gradual reduction of their identification potential. In particular, generalization gradually reduces the level of detail contained in the data and noise injection gradually increases the level of error added to the data.
- The key question in this situation is how much along gradual scale a data set has to be transformed in order to prevent direct and indirect identification, respectively.
- Unfortunately, there is a lack of methods that could yield any certain answers to this question. While there are some “privacy models” that attempt to address the question, they all are limited in scope and focus on just one of many ways of linking.
- Although these transformations are often referred to as anonymization techniques, they fail to guarantee that the result of the transformation is indeed anonymous.
Tools for reducing the identification potential of personal data
Implementing and applying transformations to reduce the identification potential of data can be difficult and time consuming. Most practitioners will therefore likely use already available software tools. The following provides some starting points for the search of relevant tools.
Overviews of existing tools have been provided by a multitude of players (see links to overviews in the footnotes):
- U.S. National Institute of Standards and Technology (NIST)[35],
- Aircloak[36],
- Johns Hopkins University[37],
- YourTechDiet[38], and
- Electronic Health Information Laboratory (EHIL)[39],
Note that some of the available tools must rather be considered to be tool boxes since they implement a variety of transformation concepts and algorithms. For example, the open source ARX Data Anonymization Tool by the Technical University of Munich contains both tools and a programming library that support a multitude of privacy models including k-Anonymity, ℓ-Diversity, t-Closeness, and differential privacy[40].
References
1See https://uldsh.de/PseudoAnon. ↑
2Simson L. Garfinkel, De-Identifying Government Datasets, NIST Special Publication 800-188 (2nd Draft), 2016, https://csrc.nist.gov/publications/detail/sp/800-188/draft (last visited 6/1/2021). ↑
3Fung, Benjamin & Wang, Ke & Fu, Ada & Yu, Philip, 2010, Introduction to Privacy-Preserving Data Publishing: Concepts and Techniques, DOI 10.1201/9781420091502, https://www.academia.edu/24652325/Introduction_to_Privacy_Preserving_Data_Publishing (last visited 23/12/2020). ↑
4See European Union Agency for Cybersecurity (ENISA); Athena Bourka, Prokopios Drogkaris, and Ioannis Agrafiotis (all ENISA, Editors); Meiko Jensen (Kiel University), Cedric Lauradoux (INRIA), Konstantinos Limniotis (HDPA) (contributors); Pseudonymisation techniques and best practices; Recommendations on shaping technology according to data protection and privacy provisions; November 2019; https://www.enisa.europa.eu/publications/pseudonymisation-techniques-and-best-practices (last visited 12/8/2021). ↑
5See for example https://en.wikipedia.org/wiki/Level_of_measurement#Ratio_scale (last visited 25/11/2020). ↑
6See for example https://en.wikipedia.org/wiki/Generation#Western_world (last visited 25/11/2020). ↑
7See for example ↑
8See for example https://en.wikipedia.org/wiki/Level_of_measurement#Nominal_level (last visited 25/11/2020). ↑
9See Figure 4c on page 4 in Kristen LeFevre, David J. DeWitt and Raghu Ramakrishnan, Multidimensional K-Anonymity, Technical Report 1521, Department of Computer Sciences, University of Wisconsin, Madison, Revised June 22, 2005, https://ftp.cs.wisc.edu/pub/techreports/2005/TR1521.pdf (last visited 16/12/2020). ↑
10See Samarati, P. and L. Sweeney, Protecting privacy when disclosing information: k-anonymity and its enforcement through generalization and suppression, 1998, https://dataprivacylab.org/dataprivacy/projects/kanonymity/paper3.pdf (last visited 12/8/2021). ↑
11See for example 2nd paragraph on page 3 in Garfinkel, Simson & Abowd, John & Martindale, Christian. (2019). Understanding database reconstruction attacks on public data. Communications of the ACM. 62. 46-53. 10.1145/3287287, (last visited 22/12/2020). ↑
12See footnote 34. ↑
13Xiaokui Xiao, Yufei Tao, Anatomy: Simple and Effective Privacy Preservation, VLDB 2006: 139-150, http://www.vldb.org/conf/2006/p139-xiao.pdf (last visited 22/12/2020). ↑
14Onashoga, S. A. et al. “KC-Slice: A dynamic privacy-preserving data publishing technique for multisensitive attributes.” Information Security Journal: A Global Perspective 26 (2017): 121 – 135, ↑
15N.V.S. Laskshmipathi Raju & M.N. Seetaramanath & Rao, P. Srinivasa Rao. (2018). An enhanced dynamic KC-Slice model for privacy preserving data publishing with multiple sensitive attributes by inducing sensitivity. Journal of King Saud University – Computer and Information Sciences. 10.1016/j.jksuci.2018.09.013, https://www.sciencedirect.com/science/article/pii/S1319157818304324 (last visited 23/12/2020). ↑
16See page 3 of Simson L. Garfinkel, De-Identifying Government Datasets, NIST Special Publication 800-188 (2nd Draft), 2016, https://csrc.nist.gov/publications/detail/sp/800-188/draft (last visited 6/1/2021). ↑
17Fienberg, S. and J. McIntyre. “Data Swapping: Variations on a Theme by Dalenius and Reiss.” Privacy in Statistical Databases (2004), https://www.scb.se/contentassets/ca21efb41fee47d293bbee5bf7be7fb3/data-swapping-variations-on-a-theme-by-dalenius-and-reiss.pdf (last visited 12/8/2021). ↑
18Laura McKenna, 2018. “Disclosure Avoidance Techniques Used for the 1970 through 2010 Decennial Censuses of Population and Housing,” Working Papers 18-47, Center for Economic Studies, U.S. Census Bureau. https://www.census.gov/content/dam/Census/library/working-papers/2018/adrm/Disclosure%20Avoidance%20Techniques%20for%20the%201970-2010%20Censuses.pdf (last visited 11/1/2021). ↑
19Dwork, Cynthia, Frank McSherry, Kobbi Nissim, and Adam Smith. 2017. “Calibrating Noise to Sensitivity in Private Data Analysis”. Journal of Privacy and Confidentiality 7 (3):17-51. https://doi.org/10.29012/jpc.v7i3.405. ↑
20Nicolas Sartor, Explaining Differential Privacy in 3 Levels of Difficulty, aircloak blog, https://aircloak.com/explaining-differential-privacy/ (last visited 13/1/2021). ↑
21Hsu, Justin & Gaboardi, Marco & Haeberlen, Andreas & Khanna, Sanjeev & Narayan, Arjun & Pierce, Benjamin & Roth, Aaron. (2014). Differential Privacy: An Economic Method for Choosing Epsilon. Proceedings of the Computer Security Foundations Workshop. 2014. 10.1109/CSF.2014.35. https://arxiv.org/abs/1402.3329 (last visited 15/1/2021). ↑
22footnote 42. ↑
23https://en.wikipedia.org/wiki/Differential_privacy (last visited 13/8/2021). ↑
24McClure, D. and J. Reiter. “Differential Privacy and Statistical Disclosure Risk Measures: An Investigation with Binary Synthetic Data.” Trans. Data Priv. 5 (2012): 535-552, http://www.tdp.cat/issues11/tdp.a093a11.pdf (last visited 15/1/2021). ↑
25Wood, Alexandra, Micah Altman, Aaron Bembenek, Mark Bun, Marco Gaboardi, et al. 2018. Differential Privacy: A Primer for a Non-Technical Audience. Vanderbilt Journal of Entertainment &Technology Law 21 (1): 209. http://nrs.harvard.edu/urn-3:HUL.InstRepos:38323292 (last visited 13/1/2021). ↑
26Dwork C. (2008) Differential Privacy: A Survey of Results. In: Agrawal M., Du D., Duan Z., Li A. (eds) Theory and Applications of Models of Computation. TAMC 2008. Lecture Notes in Computer Science, vol 4978. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-79228-4_1, https://web.cs.ucdavis.edu/~franklin/ecs289/2010/dwork_2008.pdf (last visited 13/1/2021). ↑
27Nozari, Erfan, P. Tallapragada and J. Cortés. “Differentially Private Average Consensus with Optimal Noise Selection.” IFAC-PapersOnLine 48 (2015): 203-208. http://www.ee.iisc.ac.in/people/faculty/pavant/files/papers/C10.pdf (last visited 13/1/2021). ↑
28Raffael Bild, Klaus A. Kuhn, Fabian Prasser, SafePub: A Truthful Data Anonymization Algorithm With Strong Privacy Guarantees, Proceedings on Privacy Enhancing Technologies, 2018(1), 67-87, https://doi.org/10.1515/popets-2018-0004 (last visited 13/1/2021). ↑
29Martín Abadi, Andy Chu, Ian Goodfellow, H. Brendan McMahan, Ilya Mironov, Kunal Talwar, Li Zhang, Deep Learning with Differential Privacy, Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security (ACM CCS), pp. 308-318, 2016, DOI 10.1145/2976749.2978318, https://arxiv.org/abs/1607.00133v2 (last visited 13/1/2021). ↑
30Linknovate Team, Differential Privacy Leaders you Must Know, September 13, 2018, https://blog.linknovate.com/differential-privacy-leaders-must-know/ (last visited 15/1/2021). ↑
31John M. Abowd, Protecting the Confidentiality of America’s Statistics: Adopting Modern Disclosure Avoidance Methods at the Census Bureau, August 17, 2018, https://www.census.gov/newsroom/blogs/research-matters/2018/08/protecting_the_confi.html (last visited 15/1/2021). ↑
32JohnWWDC 2016. June, 2016.Engineering Privacy for Your Users. https://developer.apple.com/videos/play/wwdc2016/709/. (last visited 15/1/2021). ↑
33JohnWWDC 2016. June, 2016.WWDC 2016 Keynote.https://www.apple.com/apple-events/june-2016/. (last visited 15/1/2021) ↑
34JohnSee footnote 43. ↑
35Johnhttps://www.nist.gov/itl/applied-cybersecurity/privacy-engineering/collaboration-space/focus-areas/de-id/tools (last visited 21/1/2021). ↑
36Johnhttps://aircloak.com/top-5-free-data-anonymization-tools/ (last visited 21/1/2021). ↑
37Johnhttps://dataservices.library.jhu.edu/resources/applications-to-assist-in-de-identification-of-human-subjects-research-data/ (last visited 21/1/2021). ↑
38Johnhttps://www.yourtechdiet.com/blogs/6-best-data-anonymization-tools/ (last visited 21/1/2021). ↑
39Johnhttp://www.ehealthinformation.ca/faq/de-identification-software-tools/ (last visited 21/1/2021). ↑
40Johnhttps://arx.deidentifier.org/overview/privacy-criteria/ (last visited 12/8/2021). ↑
